[CS Study] 알고리즘 (1) - 정렬 알고리즘

시작하기 전에

첫 번째 챕터는 정렬 알고리즘입니다. 여러 가지 정렬 알고리즘들을 알아봅시다.

공부하는 데 많은 도움을 받은 '기술면접대비 CS전공 핵심요약집' 저자분께 감사드립니다.

사진들의 출처는 아래와 같습니다:
https://gmlwjd9405.github.io/

---

버블 정렬이란?

버블 정렬(Bubble Sort)은 양옆에 위치한 두 값을 비교하면서 크기 순으로 정렬한다.

버블 정렬하면 배열의 뒤에서부터 정렬된다.

 

배열의 n번째 요소를 정렬하는 데 n-1번 필요하므로 배열의 모든 요소를 정리하려면 (n-1)+(n-2)+...+2+1 = n(n-1)/2 만큼 연산을 수행해야 한다. 따라서 O(n^2)의 시간 복잡도를 가진다.

---

선택 정렬이란?

선택 정렬(Selection Sort)은 배열을 순회하면서 배열의 앞에서부터 차례대로 각 인덱스에 들어갈 값을 선택해 위치시킨다.

인덱스 i에 들어갈 값을 선택하는 경우에 i-1까지는 정렬이 완료된 상태다.

 

배열의 크기를 n이라고 할 때, 각 인덱스 i에 들어갈 숫자를 찾기 위해 n-i개의 값을 비교한다. 따라서 배열 전체에 대한 정렬을 완료하려면 (n-1)+(n-2)+...+2+1 = n(n-1)/2 만큼 연산을 수행해야 한다. 따라서 O(n^2)의 시간 복잡도를 가진다.

---

삽입 정렬이란?

삽입 정렬(Insertion Sort)은 배열을 앞에서부터 순회하면서 정렬된 부분의 적절한 위치에 값을 삽입하는 방식이다.

인덱스 i에 있는 숫자를 정렬할 차례일 때, 인덱스 0부터 i-1까지는 이미 정렬된 상태다.

 

전체 배열을 순회하며 각 순회에서 인덱스 i 요소를 적절한 위치에 삽입하기 위해 최대 n-i번을 탐색한다. 따라서 마찬가지로 O(n^2)의 시간 복잡도를 가진다.

---

합병 정렬이란?

합병 정렬(Merge Sort)은 재귀를 이용하는 분할 정복 알고리즘이다.

정렬하려는 배열을 크기가 0 또는 1이 될 때까지 절반씩 분할한다. 분할된 각각의 배열은 다시 하나의 배열로 합쳐지면서 정렬을 수행한다.

 

배열의 분할 시 시간 복잡도가 O(logn)이고, 배열의 정렬 및 병합 시 시간 복잡도가 O(n)이라 총 O(nlogn)의 시간 복잡도가 소요된다.

수행 시간 면에서 효율적임을 알 수 있다.

 

※ O(logn), O(n)인 이유를 더 자세히 알고 싶다면

※ O(logn), O(n)인 이유를 더 자세히 알고 싶다면

 

1. 분할 단계:

배열을 반으로 나누는 작업을 생각하자.

한 번 나눌 때 걸리는 시간이 거의 없다. => O(1)

약 \(log_2 n\) 번 나눠야 한다. => O(logn)

따라서 배열의 분할 단계에서 O(logn)이 소요된다.

 

2. 정렬 및 병합 단계:

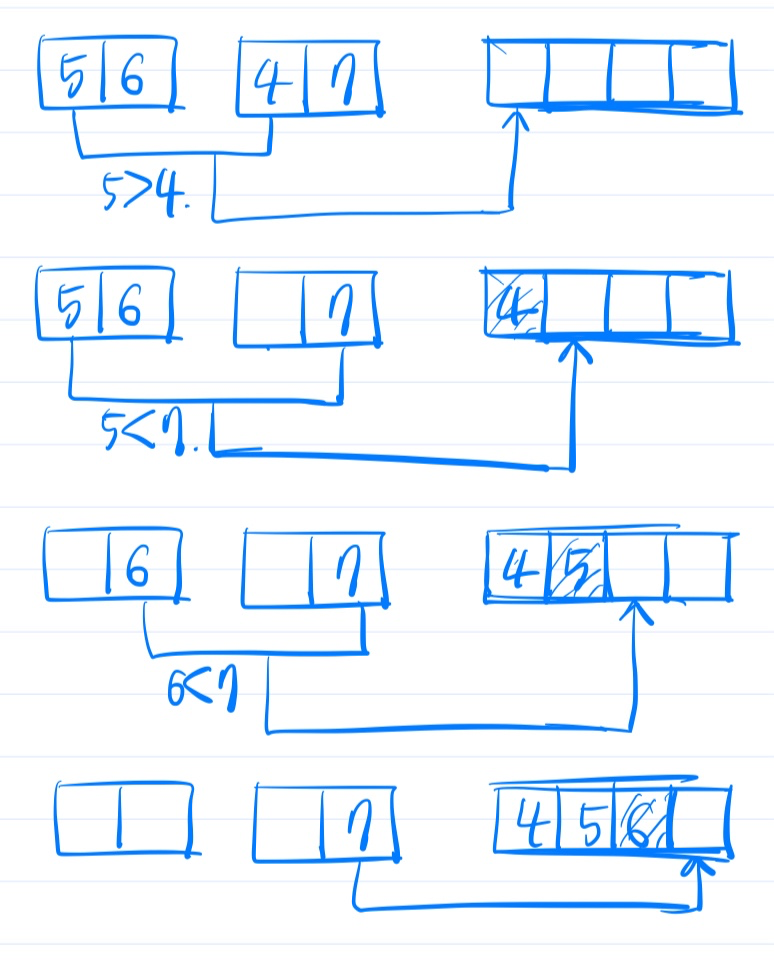
위의 그림을 보면, 각 단계에서 모든 원소를 한 번씩 방문하며 병합하기 때문에 한 단계당 병합 작업에 드는 시간은 O(n)이 소요됨을 확인할 수 있다.

---

퀵 정렬이란?

퀵 정렬(Quick Sort)은 피봇(pivot)이라는 특정 값을 선택해 피봇보다 작은 값으로 구성된 배열과 피봇보다 큰 값으로 구성된 배열로 분할해 정렬한다. 현재 가장 많이 사용되는 정렬 알고리즘이고 웬만한 경우에 가장 효율적이다. 하지만 과정이 복잡하니 그림을 상세히 보면서 이해하는 것을 추천한다.

 

합병 정렬과 마찬가지로 분할 정복 알고리즘이다. 이에 따라 시간 복잡도는 평균적으로 O(nlogn)이다.

하지만 역순으로 정렬된 배열 [5, 4, 3, 2, 1]에서 첫 번째 요소인 5를 피봇으로 선택하는 경우를 생각해보면, 5보다 큰 숫자가 없으므로 배열이 분할되지 않는다. 이와 같이 피봇 선정에 따라 최악의 경우 O(n^2)이 소요될 수도 있다.

---

힙 정렬이란?

힙 정렬(Heap Sort)은 최대 힙이나 최소 힙 자료구조를 이용해 정렬을 수행한다.

마찬가지로 방식이 조금 복잡하기 때문에 그림을 상세히 보면서 이해하자.

먼저 배열을 힙으로 만드는 과정을 수행한다.

[7, 4, 5, 6, 3, 1, 2]를 오름차순으로 힙 정렬하기 위해 최대 힙을 구성한다.

노드 4보다 자식 노드 6의 우선순위가 더 높으므로 위치를 교환한다. 그러면 최대 힙을 만족한다.

 

생성한 최대 힙에서 삭제 연산을 이용해 정렬을 수행한다. 삭제 연산으로 꺼낸 루트 노드의 값을 힙의 마지막 노드가 있던 자리로 이동한다.이 과정을 노드 개수만큼 반복하면 정렬이 완료된다.

 

힙 생성 알고리즘을 수행하는 데 O(logn)이, 전체 요소가 n개여서 전체 정렬하는 데 총 O(nlogn)의 시간 복잡도가 소요된다.

---

마치며

여러 정렬 알고리즘을 살펴봤습니다. 다음 글에서는 최소 신장 트리를 공부해보겠습니다.