시작하기 전에
이번에 Google Maching Learning Bootcamp에 붙었다. 퀄리티 있는 강의와 과제가 주어지니, 개념을 제대로 정리하고 과제를 통해 이를 활용하는 방법까지 정리하고자 한다. 추가로 내 지식, 리서치도 포함되었다.
I. Introduction to Deep Learning
딥러닝이 뭘까?
딥러닝의 개념을 알기 위해서 비슷한 개념인 데이터 분석, 머신러닝과 비교해보겠다. 모두 데이터를 분석하고 활용하는 툴이며 다 익숙한 단어지만 각각의 특징은 헷갈리는 경우가 많다.
데이터 분석
- 데이터를 검토하여 결론을 도출하고 의사 결정을 지원하는 과정이다.
- 통계적 방법, 시각화 도구, 그리고 분석 모델이 사용된다.
- 다른 둘보다 기술적 복잡성은 낮지만, 비즈니스 의사 결정에 직접적인 기여를 한다.
머신러닝
- 데이터로부터 학습할 수 있는 알고리즘을 사용하여 모델을 만드는 분야다.
- 지도학습, 비지도학습, 강화학습 등 여러 유형이 있다.
- 주로 예측 모델링과 패턴 인식에 사용되며, 비교적 복잡한 데이터셋에서 의미있는 결과를 도출할 수 있다.
딥러닝
- 머신러닝의 한 분야로, 인공 신경망을 사용하여 매우 복잡한 데이터의 패턴을 학습한다.
- 일반적으로 큰 데이터셋과 고성능 컴퓨팅 리소스를 필요로 한다.
- 이미지 인식, 음성 인식, 자연어 처리 등과 같은 고도의 문제를 해결하는 데 특히 효과적이다.
참고로 뒤에서 인공 신경망, Neural Networks 얘기가 많이 나온다.
II. Neural Networks Basics
Binary Classification

입력 이미지를 받아 Neural Network를 지나서 결과값을 1(고양이다) 또는 0(고양이가 아니다)으로 나타내는 것이다.
이미지를 입력받는 과정
컴퓨터가 인식할 수 있는 형태는 0110101... 같은 이진법이다. 이미지를 이러한 형태로 변화시켜줘야 한다.

컬러 이미지라면 Red, Green, Blue 3가지 색깔의 조합으로 이루어져 있기 때문에 쪼갤 수 있고, 특정 픽셀이 갖는 Red, Green, Blue 색상값을 각각 0~255의 숫자로 나타낼 수 있다. 그리고 이를 모두 (\( n_{x} \), 1) 차원으로, 즉 일렬로 바꾼다. 예시로, 만약 이미지가 64*64 픽셀이었다면 \( n_{x} \)는 64*64*3(RGB)가 된다.

그렇게 하면 training examples로 m개의 이미지가 들어왔을 때 X를 (\( n_{x} \), m) 차원으로 나타낼 수 있다.
Logistic Regression
한글로는 로지스틱 회귀, 수학을 사용하여 두 데이터 간의 관계를 찾는 데이터 분석 기법이다. 그 중 하나를 살펴보겠다.
Sigmoid 함수
Binary Classification에서는 Neural Network를 지났을 때 결과값이 0~1로 표현돼야 이미지가 고양이가 맞는지 판단할 수 있다. 하지만 현재 상황으로는 결과값이 0~1에 위치할 것이라는 보장이 없다. 여기서 나오는 개념이 Sigmoid이다.

Sigmoid 함수를 통해 결과값을 0~1로 만들어줄 수 있다. 식은 아래와 같다.
$$ \sigma \left( x \right) = \frac{1}{1+e^{-x}} $$
결론은 아래와 같다.
$$ \hat{y} = \sigma \left( w^{T}x + b \right) = \sigma \left( z \right) $$
※ 갑자기 모르는 개념이 많아요
※ 갑자기 모르는 개념이 많아요
하나하나 살펴보자.
- \( \hat{y} \)는 우리가 모델을 거쳐 예측을 통해 얻은 결과값이다. 실제 결과값 \( y \)와 구분하기 위해 위에 hat을 씌운다.
- \( w \)와 \( b \)는 parameter로, 각각 가중치와 편향을 나타낸다. Neural Networks는 여러 개의 layer가 있고 하나의 layer를 지날 때마다 \( w \)가 곱해지고 \(b\)가 더해지는, 가중치와 편향이 적용된다.
- \( w^{T} \)의 \( T \)는 Transpose이다. 간단하게 (a, b) 차원인 행렬에 Transpose를 하면, (b, a) 차원이 된다.
- Transpose를 왜 적용하냐고 하면, 행렬의 곱셈에서는 아래 그림의 예시에서 \( a_{2} \)와 \( b_{1} \)이 같아야 한다는 특징이 있기 때문이다. 따라서 Transpose를 통해 저 둘을 같게 맞춰주는 것이다.

- Transpose가 의미가 있는지 한 번 생각해보자. 위에서 살펴봤듯이 \(X \in \mathbb{R}^{n_{x} \times m} \), \( y \in \mathbb{R}^{1 \times m} \)이었고, \( w \in \mathbb{R}^{n_{x}} \), \( b \in \mathbb{R} \)이다.
- \( b \)를 더해주는 과정에서 차원이 안 맞는다고 생각할 수 있다. 상수 \( b \)는 스칼라 값이므로 0차원 이다. 이러한 스칼라 값을 행렬에 더해줄 때 Broadcasting 개념이 활용되어 \( w^{T}x \) 행렬의 모든 요소 값들에 \( b \)가 동일하게 더해진다.
- \( z \)는 활성화 함수가 적용되기 전에 가중치와 편향 간의 선형 결합이다. 그리고 선형 결합이란 \( a_{1}v_{1} + a_{2}v_{2} = 2[1, 2] + 1[3, 4] = [5, 8] \) 같이 벡터와 스칼라 계수를 활용하여 새로운 벡터를 생성하는 연산이다.
Cost Function
이는 각 데이터에서 나오는 Loss Function 값들의 총합이다. 따라서 우선, Loss Function이 무엇인지부터 보자.
Loss를 줄여가는 과정이 AI의 학습이다. Binary Classification에서 Loss Function은 아래와 같다. 다시 한 번 얘기하자면, \( \hat{y} \), \( y \) 2개가 함수의 입력값으로 들어가는 이유는 \( \hat{y} \)는 우리가 예측하는 값, \( y \)는 실제 값이기 때문이다.
$$ \mathcal{L} \left( \hat{y}, y \right) = - \left( ylog\hat{y} + \left( 1-y \right)log\left( 1-\hat{y} \right) \right) $$
만약 \( y \)가 1이라면, \( \mathcal{L} \left( \hat{y}, y \right) = -log\hat{y} \)이다. 그럼 실제 결과가 고양이가 맞다고 하고 있기 때문에 Loss 값을 작게 만들려면 \( \hat{y} \)이 커야 한다. 크다는 것은 1에 가까워져 가는 것이므로 실제 결과와 일치하는 방향으로 예측값이 이동한다.
반대로 만약 \( y \)가 0이라면, \( \mathcal{L} \left( \hat{y}, y \right) = -log\left( 1-\hat{y} \right) \)이다. Loss 값을 작게 만들려면 \( \hat{y} \)가 작아져야 하고 이는 0에 가까워져 가는 것이므로 마찬가지로 예측값이 실제 결과와 일치하는 방향으로 이동하는 것이다.
마지막으로 Cost Function은 이러한 Loss의 총합이므로 아래와 같다.
$$ \mathcal{J} \left( w, b \right) = \frac{1}{m} \sum^{m}_{i=1} \mathcal{L} \left( \hat{y}^{\left( i \right)}, y^{\left( i \right)} \right) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log \hat{y}^{(i)} + (1 - y^{(i)}) \log (1 - \hat{y}^{(i)}) \right] $$
Gradient Descent
그렇다면 \( \mathcal{J} \left( w, b \right) \)를 최소화하는 \( w \), \( b \) 값을 찾아야 한다. 3차원으로 표현했을 때 최소인 점을 찾으면 되겠다는 방법이 Gradient Descent이다.
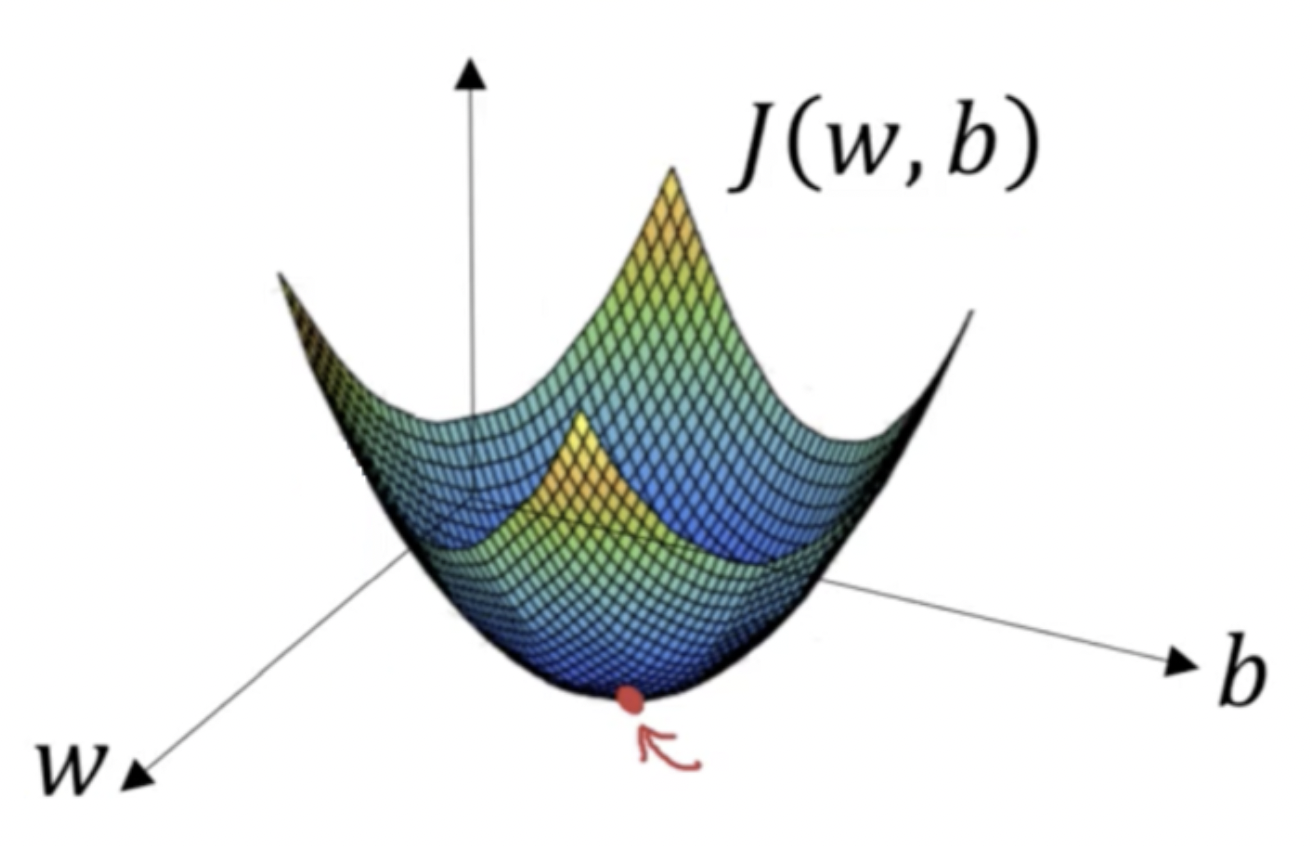
간단하게 \( w \)와 \( mathcal{J} \)의 관계에 대해서만 표현했을 때 아래 그림과 같고, 어떤 w 값에서부터 극솟점을 찾기 위해서 기울기 반대 방향으로 내려와야 하는 것을 확인할 수 있다.
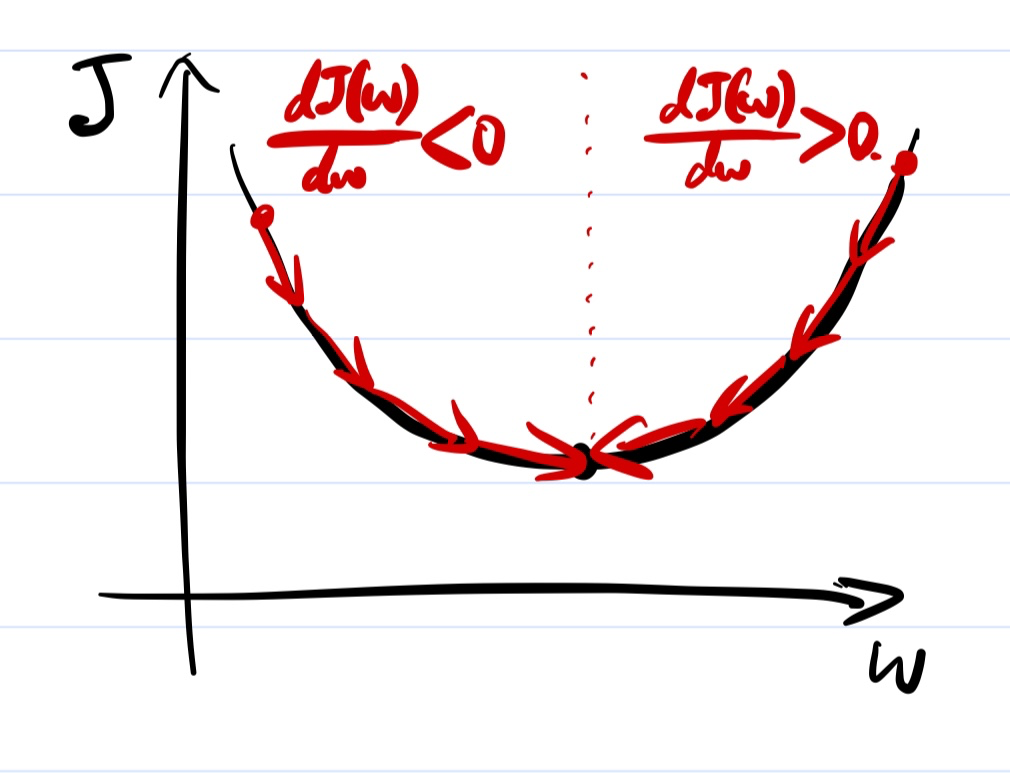
식으로 표현하면 아래와 같다. 그리고 \( b \)도 동일한 방식으로 구할 수 있겠다.
$$ w := w - \alpha \frac{d \mathcal{J} \left( w \right) }{dw} $$
$$ b := b - \alpha \frac{d \mathcal{J} \left( w \right) }{dw} $$
여기서 \( \alpha \)는 learning rate, 학습률이다. 예를 들어, 현재 w가 극솟점의 w 값보다 작은, \( \frac{d\mathcal{J}\left( w \right)}{dw} < 0 \)인 경우를 보면, w 값이 현재보다 커져야 한다. 이에 따라 기울기에 \( -\alpha \)를 곱해준 양수의 값을 w에 더해주는 것이다.
Computating Derivatives
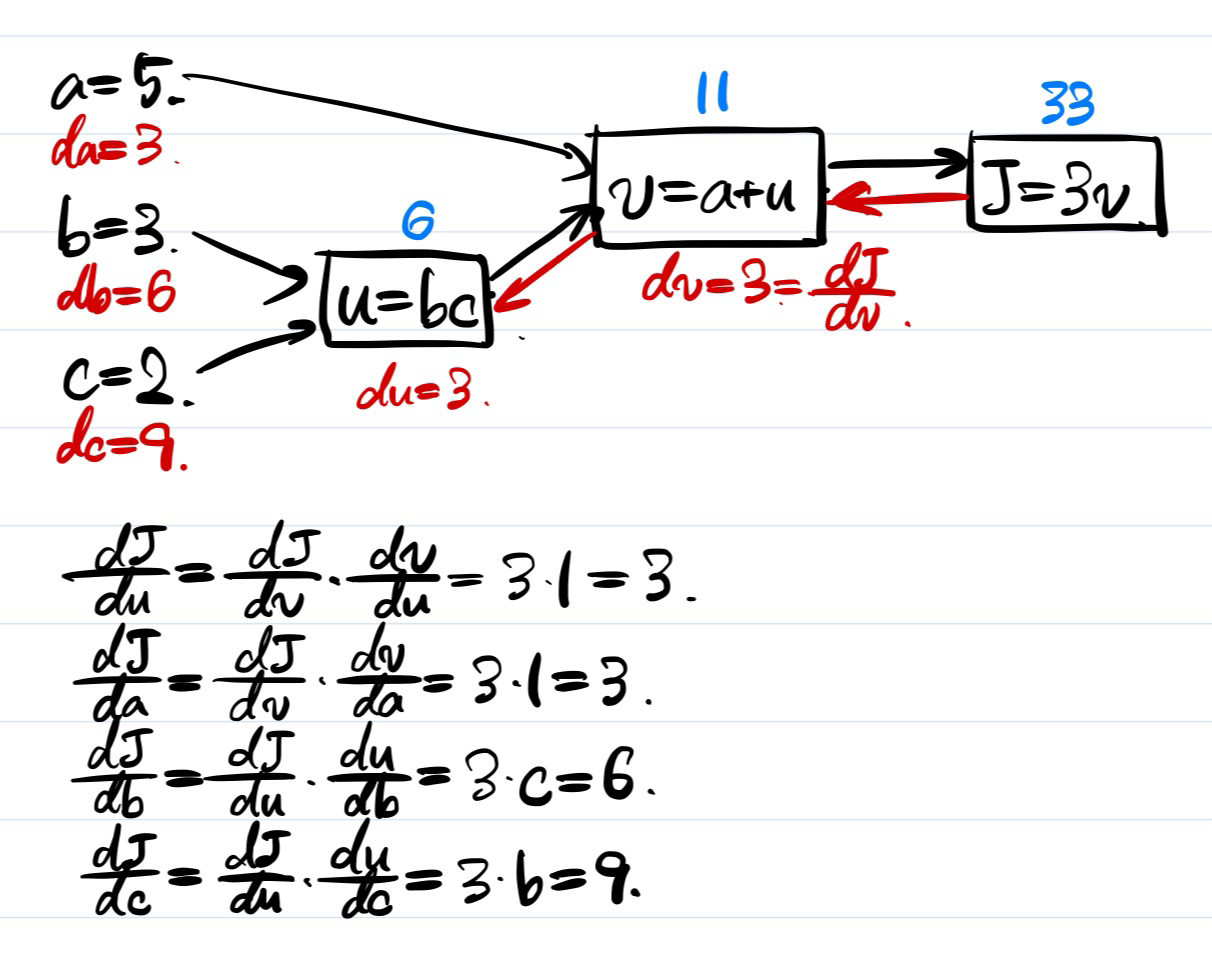
위 그림에서 a, b, c의 값에 기반하여 파란색 부분을 모두 구해낼 수 있다. 그 후에 J부터 거꾸로 돌아오면서 각각의 derivatives를 계산할 수 있다. Chain rule을 활용해서 계산하는 방법을 살펴보자.
Vectorization
Vectorization은 굉장히 중요한 테크닉이다. 예를 들어, \( w_{1} \), \( w_{2} \), ... 등에 대해 동일한 연산을 여러 번 시행해야 하는 상황이 있을 때 이를 하나의 벡터로 합쳐서 계산하면 한 방에 가능하다. 뒤에서 여러 활용 사례를 볼 수 있을 것이다.
마치며
다음 글에서는 III, IV를 정리하며 코스 1을 마무리하겠다.
'AI' 카테고리의 다른 글
| [머신러닝] Neural Networks and Deep Learning (2) (0) | 2024.07.18 |
|---|
